In our everyday experience, waves are formed by motion within a medium. Waves come in different varieties. Ocean waves and sound waves roll outward from a source through the medium of water and air. A
violin string waves back and forth along its length, held in place at the two ends of the medium, which is the violin string. A jerk on a loose rope will send a wave rolling along its length.

In 1802, Thomas Young demonstrated fairly convincingly that light had the properties of a wave. He did this by shining light through two slits, and noting that an interference pattern formed on a projection screen. Interference patterns are one of the signature characteristics of waves: two wave crests meeting will double in size; two troughs meeting will double in depth; a crest and a trough meeting will cancel eachother out to flatness. As wave ripples cross, they create a recognizable pattern, exactly matching the pattern on Young's projection screen.
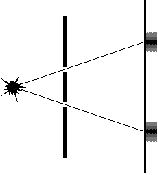
If light were made of particles, they would travel in straight lines from the source and hit the screen in two places.

If light traveled as waves, they would spread out, overlap, and form a distinctive pattern on the screen.
For most of the 19th century, physicists were convinced by Young's experiment that light was a wave. By implication, physicists were convinced that light must be traveling through some medium. The medium was dubbed "luminiferous ether," or just ether. Nobody knew exactly what it was, but the ether had to be there for the unshakably logical reason that without some medium, there could be no wave.
In 1887, Albert Michelson and E.W. Morley demonstrated fairly convincingly that there is no ether. This seemed to imply that there is no medium through which a light "wave" travels, and so there is no medium that can even form a light "wave." If this is true, how can we see evidence of waves at all? Ordinary waves of whatever sort require a medium in order to exist. The Michelson-Morley experiment should have had the effect of draining the bathtub: what kind of waves can you get with an empty bathtub? Yet the light waves still seemed to show up in the Young double slit experiment.

Without the medium, there is no wave. Only a *klunk*.
In 1905, Albert Einstein showed that the mathematics of light, and its observed constancy of speed, allowed one to make all necessary calculations without ever referring to any medium. He therefore did away with the ether as a concept in physics because it had no mathematical significance. He did not, however, explain how a wave can exist without a medium. From that point on, physicists simply put the question on the far back burner. As Michio Kaku puts it, "over the decades we [physicists] have simply gotten used to the idea that light can travel through a vacuum even if there is nothing to wave."[1]
The matter was further complicated in the 1920s when it was shown that objects -- everything from electrons to the chair on which you sit -- exhibit exactly the same wave properties as light, and suffer from exactly the same lack of any medium.
The First Computer Analogy. One way to resolve this seeming paradox of waves without medium is to note that there remains another kind of wave altogether. A wave with which we are all familiar, yet which exists without any medium in the ordinary sense. This is the computer-generated wave. Let us examine a computer-generated sound wave.
Imagine the following set up. A musician in a recording studio plays a synthesizer, controlled by a keyboard. It is a digital synthesizer which uses an algorithm (programming) to create nothing more than a series of numbers representing what a sampling of points along the desired sound wave would look like if it were played by a "real" instrument. The synthesizer's output is routed to a computer and stored as a series of numbers. The numbers are burned into a disk as a series of pits that can be read by a laser -- in other words, a CD recording. The CD is shipped to a store. You buy the CD, bring it home, and put it in your home entertainment system, and press the play button. The "music" has traveled from the recording studio to yourliving room. Through what medium did the music wave travel? To a degree, you might say that it traveled as electricity through the wires from the keyboard to the computer. But you might just as well say it traveled by truck along the highway to the store. In fact, this "sound wave" never existed as anything more than a digital representation of a hypothetical sound wave which itself never existed. It is, first and last, a string of numbers. Therefore, although it will produce wave like effects when placed in your stereo, this wave never needed any medium other than the computer memory to spread itself all over the music loving world. As you can tell from your CD collection, computers are very good at generating, storing, and regenerating waves in this fashion.
Calculations from an equation [here, y = sin (x) + sin (2.5 x)] produce a string of numbers, i.e., 1, 1.5, 0.4, 0, 0.5, 1.1, 0.3, -1.1, -2, -1.1, 0.1, and 0.5.
These numbers can be graphed to create a picture of the wave that would be created by combining (interfering) the two simple sine waves.
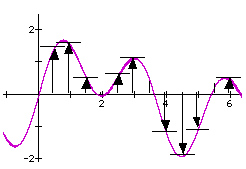
By analogizing to the operations of a computer, we can do away with all of the conceptual difficulties that have plagued physicists as they try to describe how a light wave -- or a matter wave -- can travel or even exist in the absence of any medium.
B. Waves of calculation, not otherwise manifest, as though they really were differential equations
The more one examines the waves of quantum mechanics, the less they resemble waves in a medium. In the 1920s, Ernst Schrodinger set out a formula which could "describe" the wave-like behavior of all quantum units, be they light or objects. The formula took the form of an equation not so very different from the equations that describe sound waves or harmonics or any number of things with which Isaac Newton would have been comfortable. For a brief time, physicists sought to visualize these quantum waves as ordinary waves traveling through some kind of a medium (nobody knew what kind) which somehow carried the quantum properties of an object. Then Max Born pointed out something quite astonishing: the simple interference of these quantum waves did not describe the observed behaviors; instead, the waves had to be interfered and the mathematical results of the interference had to be further manipulated (by "squaring" them, i.e., by multiplying the results by themselves) in order to achieve the final probability characteristic of all quantum events. It is a two-step process, the end result of which requires mathematical manipulation. The process can not be duplicated by waves alone, but only by calculations based on numbers which cycled in the manner of waves.
From Born, the Schrodinger wave became known as a probability wave (although actually it is a cycling of potentialities which, when squared, yield a probability). Richard Feynman developed an elegant model for describing the amplitude (height or depth representing the relative potentiality) of the many waves involved in a quantum event, calculating the interference of all of these amplitudes, and using the final result to calculate a probability. However, Feynman disclaimed any insight into whatever physical process his system might be describing. Although his system achieved a result that was exactly and perfectly in accord with observed natural processes, to him it was nothing more than calculation. The reason was that, as far as Feynman or anybody else could tell, the underlying process itself was nothing more than calculation.
The Second Computer Analogy. A process that produces a result based on nothing more than calculation is an excellent way to describe the operations of a computer program. The two-step procedure of the Schrodinger equation and the Feynman system may be impossible to duplicate with physical systems, but for the computer it is trivial. That is what a computer does -- it manipulates numbers and calculates. (As we will discuss later, the computer must then interpret and display the result to imbue it with meaning that can be conveyed to the user.)
Wave summary. Quantum mechanics involves "waves" which cannot be duplicated or even approximated physically; but which easily can be calculated by mathematical formula and stored in memory, creating in effect a static map of the wave shape. This quality of something having the appearance and effect of a wave, but not the nature of a wave, is pervasive in quantum mechanics, and so is fundamental to all things in our universe. It is also an example of how things which are inexplicable in physical terms turn out to be necessary or convenient qualities of computer operations.
II. The Measurement Effect
A. "Collapse of the wave function" -- consciousness as mediator, as though the sensory universe was a display to the user
During the course of an observation of a quantum event, the wave-like nature of the quantum unit is not observed. The evidence for the existence of quantum waves is entirely inferential, derived from such phenomena as the interference pattern on Mr. Young's projection screen. After analyzing such a phenomenon, the conclusion is that the only thing that could cause such a pattern is a wave. ("It is as if two waves were interfering.") However, actual observation always reveals instead a particle. For example, as instruments were improved, it turned out that the interference pattern observed by Young was created not by a constant sloshing against the projection screen, but by one little hit at a time, randomly appearing at the projection screen in such a way that over time the interference pattern built up. "Particles" of light were being observed as they struck the projection screen; but the eventual pattern appeared to the eye, and from mathematical analysis, to result from a wave.
Particles of Light
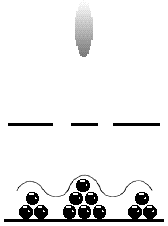
This presents conceptual difficulties that are almost insurmountable as we attempt to visualize a light bulb (or laser or electron gun) emitting a particle at the source location, which immediately dissolves into a wave as it travels through the double slits, and which then reconstitutes itself into a particle at the projection screen, usually at a place where the (presumed) overlapping wave fronts radiating from the two slits reinforce each other. What is more, this is only the beginning of the conceptual difficulties with this phenomenon.
Investigating the mechanics of this process turns out to be impossible, for the reason that whenever we try to observe or otherwise detect a wave we obtain, instead, a particle. The very act of observation appears to change the nature of the quantum unit, according to conventional analysis. Variations on the double slit experiment provide the starkest illustration.
If we assume that quantum units are particles, it follows that the particle must travel from the emission source, through one slot or the other, and proceed to the projection screen. Therefore, we should be able to detect the particle mid-journey, i.e., at one slot or the other. The rational possibilities are that the particle would be detected at one slot, the other slot, or both slots.
Experiment shows that the particle in fact is detected always at one slot or the other slot, never at both slots, seeming to confirm that we are indeed dealing with particles.
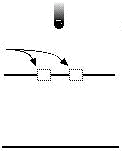
Placing electron detectors at the slots.
However, a most mysterious thing happens when we detect these particles at the slots: the interference patterns disappears and is replaced by a clumping in line with the source and the slots. Thus, if we thought that some type of wave was traveling through this space in the absence of observation, we find instead a true particle upon observation -- a particle which behaves just like a particle is supposed to behave, to the point even of traveling in straight lines like a billiard ball.
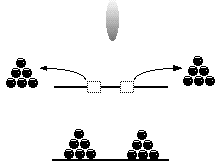
Results if electrons are detected at the slots.
To further increase the mystery, it appears that the change from wave to particle takes place not upon mechanical interaction with the detecting device, but upon a conscious being's acquiring the knowledge of the results of the attempt at detection. Although not entirely free from doubt, experiment seems to indicate that the same experimental set up will yield different results (clumping pattern or interference pattern at the projection screen) depending entirely on whether the experimenter chooses to learn the results of the detection at the slits or not. This inexplicable change in behavior has been called the central mystery of quantum mechanics.
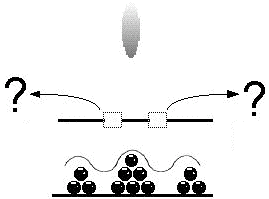
Results if electrons are NOT detected at the slots.
At the scientific level, the question is "how?" The conventional way of describing the discrepancy between analysis and observation is to say that the "wave function" is somehow "collapsed" during observation, yielding a "particle" with measurable properties. The mechanism of this transformation is completely unknown and, because the scientifically indispensable act of observation itself changes the result, it appears to be intrinsically and literally unknowable.
At the philosophical level, the question is "why?" Why should our acquisition of knowledge affect something which, to our way of thinking, should exist in whatever form it exists whether or not it is observed? Is there something special about consciousness that relates directly to the things of which we are conscious? If so, why should that be?
The computer analogy. As John Gribbin puts it, "nature seems to 'make the calculation' and then present us with an observed event."[2] Both the "how" and the "why" of this process can be addressed through the metaphor of a computer which is programmed to project images to create an experience for the user, who is a conscious being.
The "how" is described structurally by a computer which runs a program. The program provides an algorithm for determining the position (in this example) of every part of the image, which is to say, every pixel that will be projected to the user. The mechanism for transforming the programming into the projection is the user interface. This can be analogized to the computer monitor, and the mouse or joystick or other device for viewing one part of the image or another. When the user chooses to view one part of the image, those pixels must be calculated and displayed; all other parts of the image remain stored in the computer as programming. Thus, the pixels being viewed must follow the logic of the projection, which is that they should move like particles across the screen. The programming representing the parts of the image not being displayed need not follow this logic, and may remain as formulas. Calculating and displaying any particular pixel is entirely a function of conveying information to the user, and it necessarily involves a "change" from the inchoate mathematical relationships represented by the formula to the specific pixel generated according to those relationships. The user can never "see" the programming, but by analysis can deduce its mathematical operation by careful observation of the manner in which the pixels are displayed. The algorithm does not collapse into a pixel; rather, the algorithm tells the monitor where and how to produce the pixel for display to the user according to which part of the image the user is viewing.
The "why" is problematical in the cosmic sense, but is easily stated within the limits of our computer metaphor. The programming produces images for the user because the entire set up was designed to do just that: to present images to a user (viewer) as needed by the user. The ultimate "why" depends on the motivation of the designer. In our experience, the maker of a video game seeks to engage the attention of the user to the end that the user will spend money for the product and generate profits for the designer. This seems an unlikely motivation for designing the universe simulation in
which we work and play.
B. Uncertainty and complementary properties, as though variables were being redefined and results calculated and recalculated according to an underlying formula
We have seen one aspect of the measurement effect, which is that measurement (or observation) appears to determine whether a quantum unit is displayed or projected to the user (as a "particle"), or whether instead the phenomenon remains inchoate, unobserved, behaving according to a mathematical algorithm (as a "wave"). There is another aspect of measurement that relates to the observed properties of the particle-like phenomenon as it is detected. This is the famous Heisenberg uncertainty principle.
As with all aspects of quantum mechanics, the uncertainty principle is not a statement of philosophy, but rather a mathematical model which is exacting and precise. That is, we can be certain of many quantum measurements in many situations, and we can be completely certain that our results will conform to quantum mechanical principles. In quantum mechanics, the "uncertainty principle" has a specific meaning, and it describes the relationship between two properties which are "complementary," that is, which are linked in a quantum mechanical sense (they "complement" each other, i.e., they are counterparts, each of which makes the other "complete").
The original example of complementary properties was the relationship between position and momentum. According to classical Newtonian physics and to common sense, if an object simply exists we should be able to measure both where it is and how fast it is moving. Measuring these two properties would allow us to predict where the object will be in the future. In practice, it turns out that both position and momentum cannot be exactly determined at the same moment -- a discovery that threw a monkey wrench into the clockwork predictability of the universe. Put simply, the uncertainty relationship is this: for any two complementary properties, any increase in the certainty of knowledge of one property will necessarily lead to a decrease in the certainty of knowledge of the other property.
The uncertainty principle was originally thought to be more statement of experimental error than an actual principle of any great importance. When scientists were measuring the location and the speed (or, more precisely, the momentum) of a quantum unit -- two properties which turn out to be complementary -- they found that they could not pin down both at once. That is, after measuring momentum, they would determine position; but then they found that the momentum had changed. The obvious explanation was that, in determining position, they had bumped the quantum unit and thereby changed its momentum. What they needed (so they thought) were better, less intrusive instruments. On closer inspection, however, this did not turn out to be the case. The measurements did not so much change the momentum, as they made the momentum less certain, less predictable. On remeasurement, the momentum might be the same, faster, or slower. What is more, the range of uncertainty of momentum increased in direct proportion to the accuracy of the measurement of location.
In 1925, Werner Heisenberg conducted a mathematical analysis of the position and momentum of quantum units. His results were surprising, in that they showed a mathematical incompatibility between the two properties. Heisenberg was able to state that there was a mathematical relationship between the properties p (position) and m (momentum), such that the more precise your knowledge of the one, the less precise your knowledge of the other. This "uncertainty" followed a formula which, itself, was quite certain. Heisenberg's mathematical formula accounted for the experimental results far, far more accurately than any notion of needing better equipment in the laboratory. It seems, then, that uncertainty in the knowledge of two complementary properties is more than a laboratory phenomenon -- it is a law of nature which can be expressed mathematically.
A good way to understand the uncertainty principle is to take the extreme cases. As we will discuss later on, a distinguishing feature of quantum units is that many of their properties come in whole units and whole units only. That is, many quantum properties have an either/or quality such that there is no in between: the quantum unit must be either one way or the other. We say that these properties are "quantized," meaning that the property must be one specific value (quantity) or another, but never anything else. When the uncertainty principle is applied to two complementary properties which are themselves quantized, the result is stark. Think about it. If a property is quantized, it can only be one way or the other; therefore, if we know anything about this property, we know everything about this property.
There are few, if any, properties in our day to day lives that can be only one way or the other, never in between. If we leave aside all quibbling, we might suggest the folk wisdom that "you can't be a little bit pregnant." A woman either is pregnant, or she is not pregnant. Therefore, if you know that the results of a reliable pregnancy test are positive, you know everything there is to know about her pregnancy property: she is pregnant. For a "complementary" property to pregnancy, let us use marital status. (In law, you are either married or not married, with important consequences for bigamy prosecutions.)
The logical consequence of knowing everything about one complementary property is that, as a law of nature, we then would know nothing about the other complementary property. For our example, we must imagine that, by learning whether a married woman is pregnant, we thereby no longer know whether she is married. We don't forget what we once knew; we just can no longer be certain that we will get any particular answer the next time we check on her marital status. The mathematical statement is that, by knowing pregnancy, you do not know whether she is married; and, by knowing marital status, you do not know whether she is pregnant. In order to make this statement true, if you once know her marital status, and you then learn her pregnancy status (without having you forget your prior knowledge of marital status), the very fact of her marital status must become random yes or no. A definite maybe.
What is controlling is your state of certainty about one property or the other. In just this way, the experimentalist sees an electron or some other quantum unit whose properties depend on the experimentalist's knowledge or certainty of some other complementary property.
A computer's data. If we cease to think of the quantum unit as a "thing," and begin to imagine it as a pixel, that is, as a display of information in graphic (or other sensory) form, it is far easier to conceive of how the uncertainty principle might work. The "properties" we measure are variables which are computed for the purpose of display, which is to say, for the purpose of giving the user knowledge via the interface. A computed variable will display according to the underlying algorithm each time it is computed, and while the algorithm remains stable, the results of a particular calculation can be made to depend on some other factor, including another variable.
It would be far easier to understand our changing impressions of the hypothetical woman if we knew that, although she appeared to be a person like ourselves, in fact she was a computer projection. As a computer projection, she could be pregnant or not pregnant, married or single, according to whatever rules the computer might be using to create her image.
Complementary properties are simply paired variables, the calculation of which depends on the state of the other. Perhaps they share a memory location, so that when one variable is calculated and stored, it displaces whatever value formerly occupied that location; then the other variable would have to be calculated anew the next time it was called for. In this way, or in some analogous way, we can see that the appearance of a property does not need to be related to the previously displayed value of the property, but only to the underlying algorithm.
III. The Identical/Interchangeable Nature of "Particles" and Measured Properties.
As though the "particles" were merely pictures of particles, like computer icons.
Quantum units of the same type are identical. Every electron is exactly the same as every other electron; every photon the same as every other photon; etc. How identical are they? So identical that Feynman was able seriously to propose that all the electrons and positrons in the universe actually are the same electron/positron, which merely has zipped back and forth in time so often that we observe it once for each of the billions of times it crosses our own time, so it seems like we are seeing billions of electrons.[3] If you were to study an individual quantum unit from a collection, you would find nothing to distinguish it from any other quantum unit of the same type. Nothing whatsoever. Upon regrouping the quantum units, you could not, even in principle, distinguish which was the unit you had been studying and which was another.
The complete and utter sameness of each electron (or other quantum unit) has a number of consequences in physics. If the mathematical formula describing one electron is the same as that describing another electron,
then there is no method, even in principle, of telling which is which. This means, for example, that if you begin with two quantum electrons at positions A and B, and move them to positions C and D, you cannot state whether they traveled the paths A to C and B to D, or A to D and B to C. In such a situation, there is no way to identify the electron at an end position with one or the other of the electrons at a beginning position; therefore, you must allow for the possibility that each electron at A and B arrived at either C or D. This impacts on the math predicting what will happen in any given quantum situation and, as it turns out, the final probabilities agree with this interchangeable state of affairs.
The computer analogy. Roger Penrose has likened this sameness to the images produced by a computer.[4] Imagine the letter "t." On the page you are viewing, the letter "t" appears many times. Every letter t is exactly like every other letter t. That is because on a computer, the letter t is produced by displaying a particular set of pixels on the screen. You could not, even in principle, tell one from the other because each is the identical image of a letter t. The formula for this image is buried in many layers of subroutines for displaying pixels, and the image does not change regardless of whether it is called upon to form part of the word "mathematical" or "marital".
Similarly, an electron does not change regardless of whether it is one of the two electrons associated with the helium atom, or one of the ninety-two electrons associated with the uranium atom. You could not, even in principle, tell one from another. The only way in this world to create such identical images is to use the same formula to produce the same image, over and over again whenever a display of the image is called for.
IV. Continuity and Discontinuity in Observed Behaviors
A. "Quantum leaps," as though there was
no time or space between quantum
events
In our experience, things move from one end to the other by going through the middle; they get from cold to hot by going through warm; they get from slow to fast by going through medium; and so on. Phenomena move from a lower state to a higher state in a ramp-like fashion -- continuously increasing until they reach the higher state. Even if the transition is quick, it still goes through all of the intermediate states before reaching the new, higher state.
In quantum mechanics, however, there is no transition at all. Electrons are in a low energy state on one observation, and in a higher energy state on the next; they spin one way at first, and in the opposite direction next. The processes proceed step-wise; but more than step-wise, there is no time or space in which the process exists in any intermediate state.
It is a difficult intellectual challenge to imagine a physical object that can change from one form into another form, or move from one place to another place, without going through any transition between the two states. Zeno's paradoxes offer a rigorously logical examination of this concept, with results that have frustrated analysts for millennia. In brief, Zeno appears to have "proved" that motion is not possible, because continuity (smooth transitions) between one state and the next implies an infinite number of transitions to accomplish any change whatsoever. Zeno's paradoxes imply that space and time are discontinuous -- discrete points and discrete instants with nothing in between, not even nothing. Yet the mind reels to imagine space and time as disconnected, always seeking to understand what lies between two points or two instants which are said to be separate.
The pre-computer analogy. Before computer animation there was the motion picture. Imagine that you are watching a movie. The motion on the screen appears to be smooth and continuous. Now, the projectionist begins to slow the projection rate. At some point, you begin to notice a certain jerkiness in the picture. As the projection rate slows, the jerkiness increases, and you are able to focus on one frame of the movie, followed by a blanking of the screen, followed by the next frame of the movie. Eventually, you see that the motion which seemed so smooth and continuous when projected at 30 frames per second or so is really only a series of still shots. There is no motion in any of the pictures, yet by rapidly flashing a series of pictures depicting intermediate positions of an actor or object, the effective illusion is one of motion.
The computer analogy. Computers create images in the same manner. First, they compose a still image and project it; then they compose the next still image and project that one. If the computer is quick enough, you do not notice any transition. Nevertheless, the computer's "time" is completely discrete, discontinuous, and digital. One step at a time.
Similarly, the computer's "space" is discrete, discontinuous, and digital. If you look closely at a computer monitor, you notice that it consists of millions of tiny dots, nothing more. A beautifully rendered image is made up of these dots.
The theory and architecture of computers lend themselves to a step-by-step approach to any and all problems. It appears that there is no presently conceived computer architecture that would allow anything but such a discrete, digitized time and space, controlled by the computer's internal clock ticking one operation at a time. Accordingly, it seems that this lack of continuity, so bizarre and puzzling as a feature of our natural world, is an inherent characteristic of a computer simulation.
B. The breakdown at zero, yielding
infinities, as though the universe was being run by a computer clock
on a coordinate grid
Quantum theory assumes that space and time are continuous. This is simply an assumption, not a necessary part of the theory. However, this assumption has raised some difficulties when performing calculations of quantum mechanical phenomena. Chief among these is the recurring problem of infinities.
In quantum theory, all quantum units which appear for the purpose of measurement are conceived of as dimensionless points. These are assigned a place on the coordinate grid, described by the three numbers of height, depth, and width as we have seen, but they are assigned only these three numbers. By contrast, if you consider any physical object, it will have some size, which is to say it will have its own height, width, and depth. If you were to exactly place such a physical object, you would have to take into account its own size, and to do so you would have to assign coordinates to each edge of the object.
When physicists consider quantum units as particles, there does not seem to be any easy way to determine their outer edges, if, in fact, they have any outer edges. Accordingly, quantum "particles" are designated as simple points, without size and, therefore, without edges. The three coordinate numbers are then sufficient to locate such a pointlike particle at a single point in space.
The difficulty arises when the highly precise quantum calculations are carried out all the way down to an actual zero distance (which is the size of a dimensionless point -- zero height, zero width, zero depth). At that point [sic], the quantum equations return a result of infinity, which is as meaningless to the physicist as it is to the philosopher. This result gave physicists fits for some twenty years (which is not really so long when you consider that the same problem had been giving philosophers fits for some twenty-odd centuries). The quantum mechanical solution was made possible when it was discovered that the infinities disappeared if one stopped at some arbitrarily small distance -- say, a billionth-of-a-billionth-of-a-billionth of an inch -- instead of proceeding all the way to an actual zero. One problem remained, however, and that was that there was no principled way to determine where one should stop. One physicist might stop at a billionth-of-a-billionth-of-a-billionth of an inch, and another might stop at only a thousandth-of-a-billionth of-a-billionth of an inch. The infinities disappeared either way. The only requirement was to stop somewhere short of the actual zero point. It seemed much too arbitrary. Nevertheless, this mathematical quirk eventually gave physicists a method for doing their calculations according to a process called "renormalization," which allowed them to keep their assumption that an actual zero point exists, while balancing one positive infinity with another negative infinity in such a way that all of the infinities cancel each other out, leaving a definite, useful number.
In a strictly philosophical mode, we might suggest that all of this is nothing more than a revisitation of Zeno's Achilles paradox of dividing space down to infinity. The philosophers couldn't do it, and neither can the physicists. For the philosopher, the solution of an arbitrarily small unit of distance -- any arbitrarily small unit of distance -- is sufficient for the resolution of the paradox. For the physicist, however, there should appear some reason for choosing one small distance over another. None of the theoretical models have presented any compelling reason for choosing any particular model as the "quantum of length." Because nosuch reason appears, the physicist resorts to the "renormalization" process, which is profoundly dissatisfying to both philosopher and physicist. Richard Feynman, who won a Nobel prize for developing the renormalization process, himself describes the procedure as "dippy" and "hocus-pocus." The need to resort to such a mathematical sleight-of-hand to obtain meaningful results in quantum calculations is frequently cited as the most convincing piece of evidence that quantum theory -- for all its precision and ubiquitous application -- is somehow lacking, somehow missing something. It may be that one missing element is quantized space -- a shortest distance below which there is no space, and below which one need not calculate. The arbitrariness of choosing the distance would be no more of a theoretical problem than the arbitrariness of the other fundamental constants of nature -- the speed of light, the quantum of action, and the gravitational constant. None of these can be derived from theory, but are simply observed to be constant values. Alas, this argument will not be settled until we can make far more accurate measurements than are possible today.
Quantum time. If space is quantized, then time almost surely must be quantized also. This relationship is implied by the theory of relativity, which supposes that time and space are so interrelated as to be practically the same thing. Thus, relativity is most
commonly understood to imply that space and time cannot be thought of in isolation from each other; rather, we must analyze our world in terms of a single concept -- "space-time." Although the theory ofrelativity is largely outside the scope of this essay, the reader can see from Zeno's paradoxes how space and time are intimately related in the analysis of motion. For the moment, I will only note that the theory of relativity significantly extends this view, to the point where space and time may be considered two sides of the same coin.
The idea of "quantized" time has the intellectual virtue of consistency within the framework of quantum mechanics. That is, if the energies of electron units are quantized, and the wavelengths of light are quantized, and so many other phenomena are quantized, why not space and time? Isn't it easier to imagine how the "spin" of an electron unit can change from up to down without going through anything in the middle if we assume a quantized time? With quantized time, we may imagine that the change in such an either/or property takes place in one unit of time, and that, therefore, there is no "time" at which the spin is anywhere in the middle. Without quantized time, it is far more difficult to eliminate the intervening spin directions.
Nevertheless, the idea that time (as well as space) is "quantized," i.e., that time comes in individual units, is still controversial. The concept has been seriously proposed on many occasions, but most current scientific theories do not depend on the nature of time in this sense. About all scientists can say is that if time is not continuous, then the changes are taking place too rapidly to measure, and too rapidly to make any detectable difference in any experiment that they have dreamed up. The theoretical work that has been done on the assumption that time may consist of discontinuous jumps often focuses on the most plausible scale, which is related to the three fundamental constants of nature -- the speed of light, the quantum of action, and the gravitational constant. This is sometimes called the "Planck scale," involving the "Planck time," after the German physicist Max Planck, who laid much of the foundation of quantum mechanics through his study of minimum units in nature. On this theoretical basis, the pace of time would be around 10-44 seconds. That is one billionth-of-a-billionth-of-a-billionth-of-a-billionth of a second. And that is much too quick to measure by today's methods, or by any method that today's scientists are able to conceive of, or even hope for.
Mixing philosophy, science, time, and space. We see that the branch of physics known as relativity has been remarkably successful in its conclusion that space and time are two sides of the same coin, and should properly be thought of as a single entity: space-time. We see also that the philosophical logic of Zeno's paradoxes has always strongly implied that both space and time are quantized at some smallest, irreducible level, but that this conclusion has long been resisted because it did not seem to agree with humanexperience in the "real world." Further, we see that quantum mechanics has both discovered the ancientparadoxes anew in its mathematics, and provided some evidence of quantized space and time in its essentialexperimental results showing that "physical" processes jump from one state to the next without transition. The most plausible conclusion to be drawn from all of this is that space and time are, indeed, quantized. That is, there is some unit of distance or length which can be called "1," and which admits no fractions; and, similarly, there is some unit of time which can be called "1," and which also admits no fractions.
Although most of the foregoing is mere argument, it is compelling in its totality, and it is elegant in its power to resolve riddles both ancient and modern. Moreover, if we accept the quantization of space and time as a basic fact of the structure of our universe, then we may go on to consider how both of these properties happen to be intrinsic to the operations of a computer, as discussed above at Point IV(A).
V. Non-locality
As though all calculations were in
the CPU, regardless of the location
of the pixels on the screen.
A second key issue in quantum mechanics is the phenomenon of connectedness -- the ancient concept that all things are one -- because science has come increasingly to espouse theories that are uncannily related to this notion. In physics, this phenomenon is referred to as non-locality.
The essence of a local interaction is direct contact -- as basic as a punch in the nose. Body A affects body B locally when it either touches B or touches something else that touches B. A gear train is a typical local mechanism. Motion passes from one gear wheel to another in an unbroken chain. Break the chain by taking out a single gear and the movement cannot continue. Without something there to mediate it, a local interaction cannot cross a gap.
On the other hand, the essence of non locality is unmediated action-at-a-distance. A non-local interaction jumps from body A to body B without touching anything in between. Voodoo injury is an example of a non-local interaction. When a voodoo practitioner sticks a pin in her doll, the distant target is (supposedly) instantly wounded, although nothing actually travels from doll to victim. Believers in voodoo claim that an action here causes an effect there; that's all there is to it. Without benefit of mediation, a non-local interaction effortlessly flashes across the void.[5]
Even "flashes across the void" is a bit misleading, because "flashing" implies movement, however quick, and "across" implies distance traveled, however empty. In fact, non-locality simply does away with speed and distance, so that the cause and effect simply happen. Contrary to common sense or scientific sensibility, it appears that under certain circumstances an action here on earth can have immediate consequences across the world, or on another star, or clear across the universe. There is no apparent transfer of energy at any speed, only an action here and a consequence there.
Non-locality for certain quantum events was theorized in the 1930s as a result of the math. Many years were wasted (by Einstein, among others) arguing that such a result was absurd and could not happen regardless of what the math said. In the 1960s, the theory was given a rigorous mathematical treatment by John S. Bell, who showed that if quantum effects were "local" they would result in one statistical distribution, and if "non-local" in another distribution. In the 1970s and '80s, the phenomenon was demonstrated, based on Bell's theorem, by the actual statistical distribution of experiments. For those die-hard skeptics who distrust statistical proofs, the phenomenon appears recently to have been demonstrated directly at the University of Innsbruck.[6]
More than any of the bizarre quantum phenomena observed since 1900, the phenomenon of non-locality caused some serious thought to be given to the question, "What is reality?" The question had been nagging since the 1920s, when the Copenhagen school asserted, essentially, that our conception of reality had to stop with what we could observe; deeper than that we could not delve and, therefore, we could never determine experimentally why we observe what we observe. The experimental proof of non-locality added nothing to this strange statement, but seemed to force the issue. The feeling was that if our side of the universe could affect the other side of the universe, then those two widely separated places must somehow be connected. Alternative explanations necessarily involved signals traveling backward in time so that the effect "causes the cause," which seemed far too contrived for most scientists' tastes. Accordingly, it was fair to ask whether apparent separations in space and time -- I'm in the living room, you're in the den -- are fundamentally "real"; or whether, instead, they are somehow an illusion, masking a deeper reality in which all things are one, sitting right on top of each other, always connected one to another and to all. This sounds suspiciously like mysticism, and the similarity of scientific and mystical concepts led to some attempts to import Eastern philosophy into Western science. Zukav, in particular, wants desperately to find a direct connection between science and Buddhism, but he would concede that the link remains to be discovered.
Note that the experimental results had been predicted on the basis of the mathematical formalism of quantum mechanics, and not from any prior experiments. That is, the formal mathematical description of two quantum units in certain circumstances implied that their properties thereafter would be connected regardless of separation in space or time (just as x + 2 = 4 implies that x = 2). It then turned out that these properties are connected regardless of separation in space or time. The experimentalists in the laboratory had confirmed that where the math can be manipulated to produce an absurd result, the matter and energy all around us obligingly will be found to behave in exactly that absurd manner. In the case of non-locality, the behavior is uncomfortably close to magic.
The computer analogy. The non-locality which appears to be a basic feature of our world also finds an analogy in the same metaphor of a computer simulation. In terms of cosmology, the scientific question is, "How can two particles separated by half a universe be understood as connected such that they interact as though they were right on top of each other?" If we analogize to a computer simulation, the question would be, "How can two pictures at the far corners of the screen be understood as connected such that the distance between them is irrelevant?"
In fact, the measured distance between any two pixels (dots) on the monitor's display turns out to be entirely irrelevant, since both are merely the products of calculations carried out in the bowels of the computer as directed by the programming. The pixels may be as widely separated as you like, but the programming generating them is forever embedded in the computer's memory in such a way that -- again speaking quite literally -- the very concept of separation in space and time of the pixels has no meaning whatsoever for the stored information.
VI. The Relationship of Observed
Phenomena to the Mathematical Formalism
As though physical manifestations
themselves were being produced by
a mathematical formula.
Perhaps the most striking aspect of quantum theory is the relationship of all things to the math, as with the phenomenon of non-locality discussed above, which occurs in nature, so it seems, because that is the way the equations calculate. Even though the mathematical formulas were initially developed to describe the behavior of universe, these formulas turn out to govern the behavior of the universe with an exactitude that defies our concept of mathematics. As Nick Herbert puts it, "Whatever the math does on paper, the quantumstuff does in the outside world."[7] That is, if the math can be manipulated to produce some absurd result, it will always turn out that the matter and energy around us actually behave in exactly that absurd manner when we look closely enough. It is as though our universe is being produced by the mathematical formulas. The backwards logic implied by quantum mechanics, where the mathematical formalism seems to be more "real" than the things and objects of nature, is unavoidable. In any conceptual conflict between what a mathematical equation can obtain for a result, and what a real object actually could do, the quantum mechanical experimentalresults always will conform to themathematical prediction.
Quantum theory is rooted in statistics, and such reality conflicts often arise in statistics. For example, the math might show that a "statistically average" American family has 2.13 children, even though we know that a family of real human beings must have a whole number of children. In our experience, we would never find such a statistically average family regardless of the math, because there simply is no such thing as 13/100ths of a child. The math is entirely valid, but it must yield to the census-taker's whole-child count when we get down to examining individual families. In quantum mechanics, however, the math will prevail -- as though the statistics were drawn up in advance and all American families were created equally with exactly 2.13 children, nevermind that we cannot begin to conceive of such a family. To the mathematician, these two situations are equivalent, because either way the average American family ends up with 2.13 children. But the quantum mechanical relationship of the math to the observation does not make any sense to us because in our world view, numbers are just symbols representing something with independent existence.
Mr. Herbert states that, "Quantum theory is a method of representing quantumstuff mathematically: a model of the world executed in symbols."[8] Since quantum theory describes the world perfectly -- so perfectly that its symbolic, mathematical predictions always prevail over physical insight -- the equivalence between quantum symbolism and universal reality must be more than an oddity: it must be the very nature of reality.
This is the point at which we lose our nerve; yet the task for the Western rationalist is to find a mechanical model from our experience corresponding to a "world executed in symbols."
The final computer analogy. An example which literally fits this description is the computer simulation, which is a graphic representation created by executing programming code. The programming code itself consists of nothing but symbols, such as 0 and 1. Numbers, text, graphics and anything else you please are coded by unique series of numbers. These symbolic codes have no meaning in themselves, but arbitrarily are assigned values which have significance according to the operations of the computer. The symbols are manipulated according to the various step-by-step sequences (algorithms) by which the programming instructs the computer how to create the graphic representation. The picture presented on-screen to the user is a world executed in colored dots; the computer's programming is a world (the same world) executed in symbols. Anyone who has experienced a computer crash knows that the programming (good or bad) governs the picture, and not vice versa. All of this forms a remarkably tight analogy to the relationship between the quantum math on paper, and the behavior of the "quantumstuff" in the outside world.
Great Neck, New York
May 2, 1999
Endnotes
| 1 | M. Kaku, Hyperspace, at 8n. | Back |
| 2 | J. Gribbin, In Search of Schrodinger's Cat, 111. | Back |
| 3 | J. Gleick, Genius, 122. | Back |
| 4 | R. Penrose, The Emperor's New Mind, 25-26. See also D. Eck, The Most Complex
Machine, 8-9. | Back |
| 5 | N. Herbert, Quantum Reality, 212-13. | Back |
| 6 | "Entangled Trio to Put Nonlocality to the Test," Science 283, 1429 (Mar. 5, 1999). | Back |
| 7 | N. Herbert at 41. | Back |
| 8 | N. Herbert at 41. | Back |
| Back to Top |
| Back to The Notebook of Philosophy & Physics |









