Relationships Among Phenomena at a Unitary Level

© 1997 by John Deutsch

Forward

By manipulating standard (macroscopic) formulas for the interrelationships among these phenomena, it is shown that certain equivalencies appear among them, such that power, energy, action and mass may be reduced to functions of time.

Part II consists of calculations, performed on a pocket calculator, in which the equivalencies noted in Part I are applied to standard values at the scale of the proton. These calculations produce the interesting result that the quantum of action (h) is shown to be the product of two values which appear to be related to each other by the "golden ratio," which is a classical relationship whereby the smaller part is to the larger part as the larger part is to the whole.

I. The Hierarchy of Time

1. A wavelength (lambda) is a measure of length, or distance, i.e., the distance between two "crests" of a wave. Taking the hypothesis that there exists some natural minimum unit of length, we will further hypothesize that such a minimum would constrain the value of the wavelength, such that the minimum wavelength would be equal to the minimum distance. We define this minimum distance, and, therefore, this minimum wavelength, as having a value of 1, the "unit of distance". (Actually, as we will see later, we are speaking of the absolute value of lambda_min; for now, we will simply set the value to 1.)

(1.1)

2. Rate, or velocity (such as the speed of light), multiplied by time equals distance:

(2.1)

From this, we derive:
(2.2)

and

(2.3)

Because we postulate that there is a minimum distance, there must be a solution to equation (2.1) such that

(2.4)

Thus:

(2.4.1)

(2.4.2)

(2.4.3)

where "a" represents any number.

3. The speed of light (c) is constant; it is, therefore, both a maximum and a minimum. The t in ct = lambda_min (equation (2.4)) will have a minimum value when the minimum distance (lambda_min) is divided by the maximum velocity (c). Thus:

(3.1)

4. The quantum of action (h), is defined in terms of energy (e) multiplied by time (t), i.e., 6.6260755 x 10^-27 ergs x secs. Since h is the minimum action, there is some value of e such that h = e(t_min). That value of e can be considered a minimum, so that:

(4.1)

Further, using the familiar formula e=mc² there will be some value of m such that e_min=mc². Since the c² term in this equation is fixed, we may call this minimum value of m "m_min". Then:

(4.2)

5. We may now dispense with the subscript "min" in these terms, for we will hence be dealing only with these minimum quantities. Thus:

(5.1)

From this we may infer that energy creates or becomes mass in squared time (t²), not in "simple" time (t¹). Therefore, we will tentatively call t² "real time", as opposed to t¹, which we will call "imaginary time".

6. Consider the following series:

(6.1)

The substitution of 1 for c²t² in the sixth term of the series derives from equation (2.4.2), above, bearing in mind that we are dealing solely with minimum values. Eliminating the intervening transformations, we deduce that h=m/t, which is a rate. Further:

(6.2)

From this we may infer that action creates or becomes mass in simple or imaginary time (t¹), not in squared or real time (t²).

7. We have one final minimum quantity to derive. By definition, power multiplied by time equals energy. Therefore, some minimum amount of power multiplied by t_min will equal e_min.

(7.1)

Again dropping the subscript, we will call this minimum amount of power simply "Power". Then we have the following:

(7.2)

8. We may now construct the following hierarchy, based on the progression of the time function, i.e., t^1/2, t⁰, t¹, and t², as set out in equations (7.2), (5.1) and (6.1):

(8.1)
(8.2)
(8.3)
(8.4)

9. We will assume that energy can be expressed equivalently in electrostatic units (esu's) or ergs. The formulas are set forth here:

(9.1)

(9.2)

Just as we have postulated a minimum energy in equation (4.2), so we will assume a minimum esu and a minimum erg. Thus, there exists some minimum esu and some minimum erg such that the following equations are true:

(9.1.1)

(9.2.1)

The minimum esu we will take to be the charge of the electron, which appears to be irreducible in nature. Because both esu and erg measure energy, the minima of these terms will be taken to be the same as our minimum energy, i.e., e_min. Similarly, the minimum grams will be our m_min, the minimum centimeters will be our lambda_min, and the minimum seconds will be our t_min. Dropping the subscripts for these terms, and substituting them, in the formula, for the units of mass, distance and time, we have the following:

(9.3)

We can further manipulate the erg_min side of the equation to show that:

(9.4)

Because we suppose that esu_min and erg_min are equivalent (i.e., both are representations of e_min), it follows that the second term of the function is equal to 1. Thus,

(9.5)

and, by manipulating the equation, it follows that

(9.6)

Note that this formulation permits time to be expressed as a function of mass and distance, and we may further manipulate the expression, so that

(9.7)

10. We may now put together the following series:

(10.1)

In this way we see that the wavelength, or distance, is equivalent to energy. (This echoes the quantum concept of a "vacuum" seething with energy.)

11. We can use this equivalence to state the following:

(11.1)

The speed of light can thus be seen as the universe's unit of power, which would be consistent with its constancy and its connection with time.

12. We can now build a hierarchy of time, organized in the following table:

(12.1)

(12.2)

(12.3)

(12.4)

Displayed as a single graphic, the hierarchy looks like this:

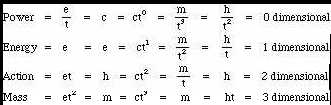
13. We can describe the same hierarchy another way by borrowing the concepts of time as the fourth dimension (from Einstein and Minkowski), and imaginary time (i.e., the square root of a negative number, as suggested by Hawking in Black Holes and Baby Universes, p. 82).

(13.1)

(13.2)

(13.3)

(13.4)

(13.5)

By this method, c = t. That is, the first and fifth powers are equivalent, setting up the circular, bounded universe suggested by Hawking. The entire system now becomes

(13.6)

In other words, 90° times 4 dimensions equals a 360° circle, where c equals t, which equals minus the square root of minus 1, via c*t⁴ = t = c*1 = c.

14. There are many interesting facets of this system. For example, note that the even powers of t produce "real" phenomena of mass and energy, while the odd powers produce the "imaginary" (or at least intangible) phenomena of power, action, and time. Also, in absolute value, energy and mass are equivalent, as are power, action and time. We may also state that, since e = lambda (equation (10.1)), and e = -1, then lambda = -1; this is why we began with the qualification (equation (1.1)) that our original lambda_min was an absolute value.

Equation (13.3) indicates that the quantum of action, h, is unique in that it can be expressed as +1/c. We will further explore the nature of h in the next section.

II. Calculations Based on Standard Values, and the Appearance of the Golden Ratio in the Quantum of Action

(15.1)

Solving for cm., we get the following:

(15.2)

Having substituted a number (-1) for the unit of distance (lambda), the result is a unitless number. Bearing in mind that we are dealing with the minimum values in nature, we may (by way of transition) think of the result as a quantity of quanta -- in this case, a quantity of negative quanta.

16. Staying with our proton model, we can take m_min to be the mass of the proton, which is 1.6726231 x 10^-24 grams. We have seen that m_min is equal to +1 (equation (13.4)). Accordingly:

(16.1)

Solving for gm., we get the following:

(16.2)

17. We will take the t_min to be the time it takes for light to travel the diameter of a proton, which will be the Compton wavelength divided by the speed of light.

(17.1)

Solving for sec., we get the following:

(17.2)

18. Let us now calculate t_min using our hierarchical system. The t_min quantity will be some number of seconds, or some fraction of a second, i.e., t_min = x sec. The m_min will be as calculated above, equation (16.1), i.e., 1.6726231 x 10^-24 gm. The quantum of action, h_min or just h, will be some number (a) of ergs times seconds, i.e., a erg.secs., which can also be expressed as a gm.cm.²/sec., from equation (9.2, multiplied by seconds). The speed of light, c, will remain as 2.9979246 x 10¹⁰ cm./sec.

We will calculate the coefficient of time for both ct = e (equation (12.2)) and for ht = m (equation (12.4)), and compare the results.

(18.1.1)

(18.1.2)

(18.1.3)

(18.2.1)

(18.2.2)

(18.2.3)

If we now equate the results of equations (18.1.3) and (18.2.3), on the theory that the coefficient of time will be the same when deriving minimum quanta, we can attempt to solve for a, which is the quantum coefficient of action, or h.

(18.3.1)

(18.3.2)

(18.3.3)

(18.3.4)

Using the value of cm. that we derived in equation (15.2), we can now solve for a, as follows:

(18.4.1)

(18.4.2)

which is, indeed, the observed value of h, within the limits of my calculator. Note that we arrived at this result by using our quantum of mass (m_proton), which is not ordinarily included in derivations of t; from this we may infer that h may be a function of mass and distance.

19. If we solve for x in both equation (18.1.3) and equation (18.2.3), substituting the values we have derived for cm. (equation (15.2)) and a (from equation (18.4.2) or, more precisely, from the CODATA table's value for h), we also arrive at the correct value for our assumed t_min, i.e. the time for light to travel the diameter of a proton from equation (17.1). Thus, the math appears to be consistent, and we can calculate both h and t using these values.

20. Having arrived at values for centimeter, gram and second (equations (15.2), (16.2) and (17.2)), we can apply these values to the standard value of h itself. First, however, we will reformulate that value slightly, as follows:

(20.1)

This reformulation produces an interesting result when the cm., gm. and sec. values are substituted:

(20.2.1)

(20.2.2)

(20.2.3)

(20.2.4)

These calculations produce the result h = 1/t, as expected from equation (13.3).

The most interesting step in this series is equation (20.2.3). Notice that, by starting with the coefficient of h times a distance squared (the left bracketed term in equation (20.1)) we have produced the inverse of a mass divided by a time (the right bracketed term in equation (20.1)). This suggests an internal structure to h. All the more interesting is the fact that these two values very closely approximate the golden ratio, which is a formulation that relates a part to the whole, and that the approximation seems to be within the limits of my pocket calculator. It goes without saying that a constant which is a function of two components that are structurally related to themselves is not itself a "fundamental" constant. Such an internal structure within h would bear out Paul Dirac's speculation that either uncertainty or probability is not, in fact, "fundamental". (P.A.M. Dirac, The Evolution of the Physicist's Picture of Nature, Scientific American, May 1963.) With further transformations, it can be shown that h can be expressed as a function of e², as Dirac had speculated.

[Back to top]
[Back to Part I]
[Back to Part II]