Commentary on Edwin Roger Banks, "Information Processing and Transmission in Cellular Automata," Banks' Ph.D. thesis, 1971 (MIT, Dep't of Mechanical Engineering).  By Ross Rhodes.

Part 2  Cellular Automata Computers

There is a particular way of conceiving of computer operations that is both extremely simple and extremely complex. The simplicity lies in the operational rules of the computations, and in the engineering structure. The complexity lies in the application of those simple rules, operating on that simple structure, as it works out in practice on the overall state of the computational system. The concept is called "cellular automata" (CA), and this is how it works.

2.1  Basic structure and operation of a CA

Fig. 2.1  The cell.


Fig. 2.2  The cell and its neighbors.

Each cell acts like a robot, an automaton, in the sense that it mindlessly follows a strict set of instructions. It acts automatically.  In this regard, the automata (automatons) of a cellular automata network are no different from any computing machine, because the PC on your desktop similarly does nothing but follow its strict set of instructions. The only difference in principle is that the PC's instructions may be vastly complex, while the cell's instructions are fixed and utterly simple.

Each cell works in this manner. Thus, although we have labeled a particular cell "C" and its eastern neighbor "E" for this illustration, that same eastern cell operates as the "C" of its own world and so takes account the states of its own neighbors (one of which is the "C" of our illustration, and the others of which are never considered by the "C" of our illustration and so have no labels).

The be-all-and-end-all of the cell's calculation is to determine what value it should take for the next round. If the cell's value for the calculation is, for example, "1," it must determine based on that value and the values of its neighbors whether to stay a "1" or to become a "0" for the next cycle of calculation.

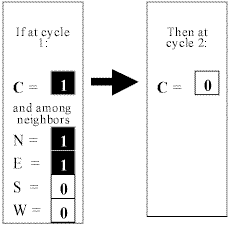
Fig. 2.3  A rule for calculation to determine the transition for cell C.

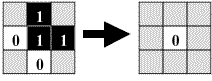
Fig. 2.4  The same rule as in fig. 2.3 represented graphically.

Each cell's completed calculation is one step of the entire array.  When everything is finished for that cycle, not only will the individual cell make a transition, but the entire cellular automata changes at one time to the new configuration reflecting all the changed cells.  From this meta-viewpoint, we see the overall CA progressing through a series of steps like frames of a movie.  Each of the many cells performs its calculations "out of sight," as it were, and nothing happens until the end of the cycle -- at which point the entire CA undergoes a single massive and total transition to a new configuration, which is the product of all of the individual cell transitions.  Then each cell starts fresh to calculate what it should do in light of its new neighbors and its own new state.

2.2  Useful things to do with a CA

Because each cell is autonomous, all of the neighbors perform the same calculation but with different data (because their north, south, east and west neighbors are different). Therefore, the next state of a cell's neighbor is impossible for the cell itself to predict because it does not have access to the neighboring cell's data. All of this yields a vastly complex series of interactions that quickly becomes impossibly difficult to predict. 

There are some famous cellular automata configurations that exhibit patterns and regular forms of interaction. Perhaps the best known is John Conway's "Game of Life," where the rules produce moving blocks of patterns. Other configurations can provide interesting models of neighbor-to-neighbor interactions such as one might find in a cloud of gas. But considering that the essential idea is based on a collection of little computing units, the early question was whether this type of array could be put to work doing general purpose computing tasks.

One of the pioneering developers of the cellular automata model of computing proved that it was possible with a cellular automata configuration to emulate the tasks of a general purpose universal computer. A drawback was that the particular configuration found by John Von Neumann required that each cell be able to take on a range of values - up to 29 different states per cell - whereas the logic that it is implementing is based on the simple yes/no two-state operation.  Later, E.F. Codd found a configuration that required only the preferred two states, but unfortunately each cell needed 84 neighbors to operate. These requirements were reduced in 1970 with Conway's Game of Life, which needed only two states and eight neighbors to achieve general purpose universal computation.

This is where the matter stood in 1970 when Roger Banks accepted Edward Fredkin's challenge of finding a simpler cellular automata that could do everything that could be done by a general purpose computer with Boolean logic gates. The challenge was to achieve this with the two-state cell interacting only with its immediate neighbors to the north, south, east and west, as used in the illustration above.